计算机科学速成

计算机早期历史

最早的计算设备：算盘，手动计算机，帮助进行加减运算，同时存储计算状态

更多计算设备诞生使得很多事情更简单，但这些设备都不是“计算机”

步进计算机：第一台可以做“加减乘除”的机器，耗时长

军队炮弹射程表

差分机、分析机的设想提出，其中分析机有了“通用计算机、自动计算机”的想法

Ada世上第一位程序员

计算机开始受到重视：美国人口普查、打孔制表机大大提高了效率，企业也开始意识到、IBM诞生

电子计算机

20世纪上叶，各行各业快速发展，计算的需求急速提高

柜子大小的计算机变成房间大小，现在又变成巴掌大小了是吧，那时的计算机维护成本极高

哈佛马克一号，1秒能做3次加法或减法运算，一次乘法要花费6秒，除法要花费15秒，放眼现在还是有些难以想象的，庞大数量的原件也伴随着磨损，故障概率的提高

哈佛马克2在故障继电器中发现一只虫子，术语bug由此而来
“From then on,when anything went wrong with a computer,we said it had bugs in it”

真空管诞生，可以取代继电器的更精巧的设备诞生，计算机由机电设备转向电子

“巨人1号”大规模使用真空管，被认为是第一个可编程的电子计算机，完成的计算比全人类还要多！Amazing!

真空管仍然伴随着高故障率和较高成本，这时在贝尔实验室中诞生了晶体管，一个全新的计算机时代诞生了！更小更偏移的计算机可以诞生了，我们可以更快的控制电路的开闭

布尔逻辑

机电设备一般十进制计数，而电子设备只用开关两种状态也可以代表信息——二进制（0，1/true，false），同时可以控制通过电流的大小，由此也可以表示不同的状态，所以也有三进制、五进制计算机的存在

采用二进制的原因：

• 状态越多越是难以区分信号
• 布尔代数（自学成才？）

布尔代数：(NOT/AND/OR/XOR)

貌似开始出现数据true/false了，也可以用过逻辑电路进行一些简单的计算了，那那些复杂的计算是如何通过这些实现的呢？

二进制

加位数即可像十进制一样表示更加庞大的数据，二进制的计算可以完全类比十进制

这里机组的知识可以发挥作用了

用二进制数表示出了整数、小数、用ASCII码规范将其表示范围进一步拓展到字符、标点

ASCII是为英语设计，所以对于不同语言，保存了一定的空位可以自己设计，但还是会出现乱码问题，Unicode由此诞生，统一编码标准

所有计算机和互联网上的信息包括声音、图像、操作系统归根结底都是一长串1和0，实现了表示和存储数字，但如何计算？实现有意义的处理数字？比如进行加减运算，算数逻辑单元！

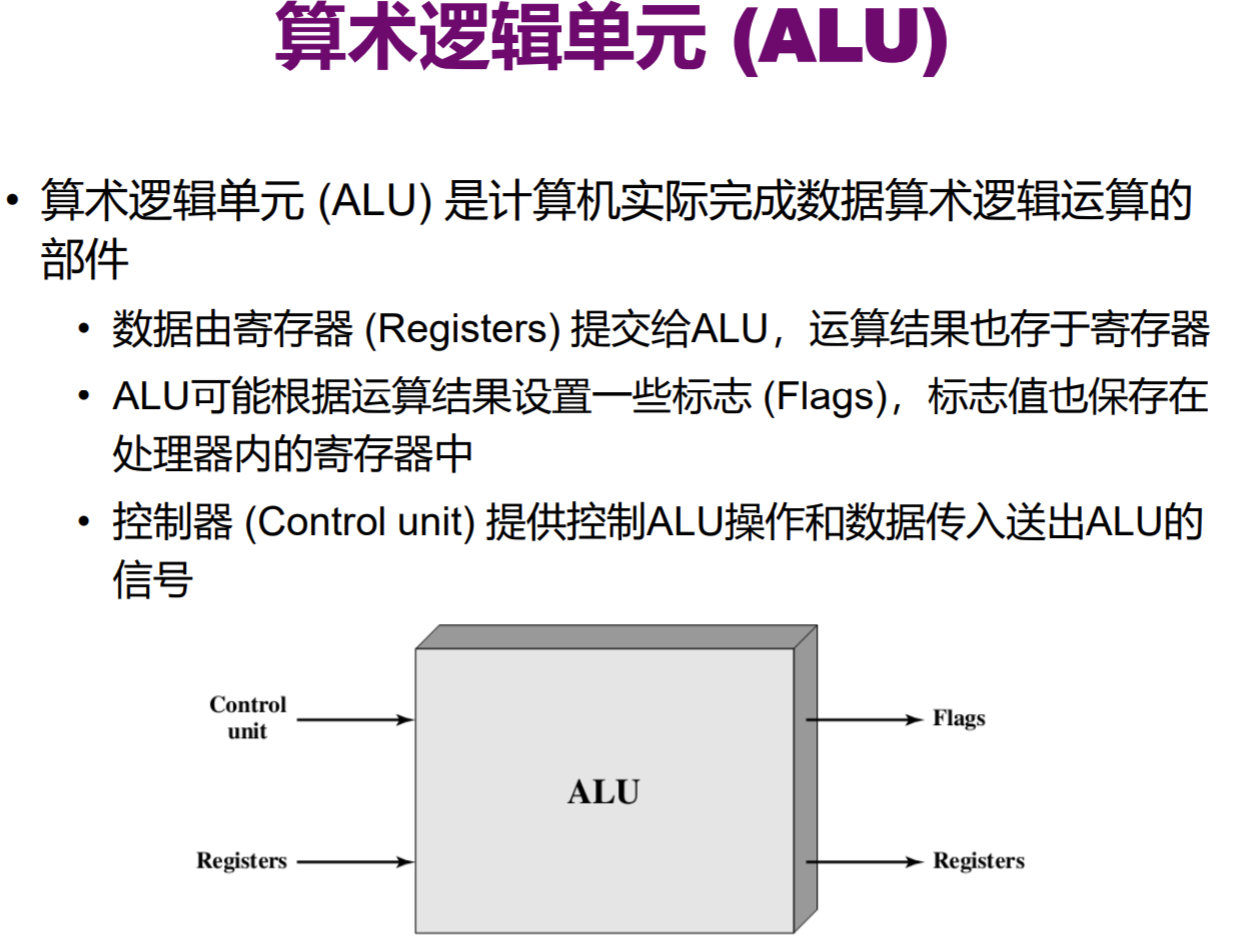
算数逻辑单元

ALU，计算机的数学大脑，计算机里负责运算的组件，基本其他所有部件都用到了他

英特尔74181，第一个封装在单个芯片的完整ALU

使用两个逻辑门实现了一位的加法运算，称为半加器

进一步抽象，使用两个半加器实现全加器

更进一步抽象，使用半加器以及全加器即可制作多位数的加法器，最后一位有进位，则表示overflow

由于计算进位有时间，提出了超前进位加法器

逻辑单元执行逻辑操作，都是一大堆逻辑门的组合

将ALU再进行抽象，得到两个输入和执行操作码，输出结果和一些标志位

附一个上学期记录的整数运算实现

整数运算

算法逻辑单元（ALU）

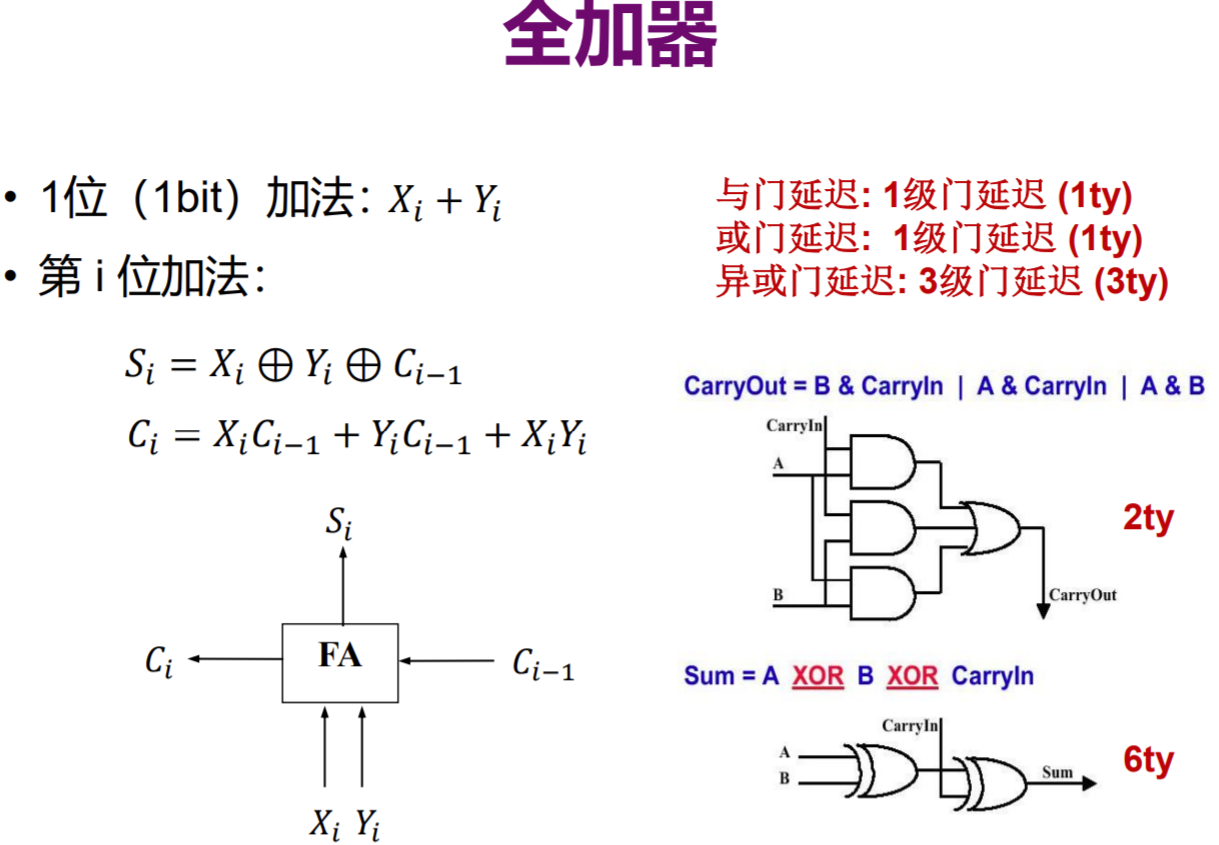
全加器

Xi	Yi	Ci-1	Ci	Si
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
1	0	0	0	1
1	1	0	1	0
1	0	1	1	0
0	1	1	1	0
1	1	1	1	1

如上图所示，进位等于三个数两两做与运算后或运算的结果，而该位的数等于三个数做异或运算

此处引出了一个极为关键的延迟，如图所示，与门以及或门延迟均为1ty，异或门延迟为3ty。

由于三个与门操作可以同时进行，所以计算Ci的总延迟为2ty；

进行两次异或操作，延迟为6ty；

进位加法器

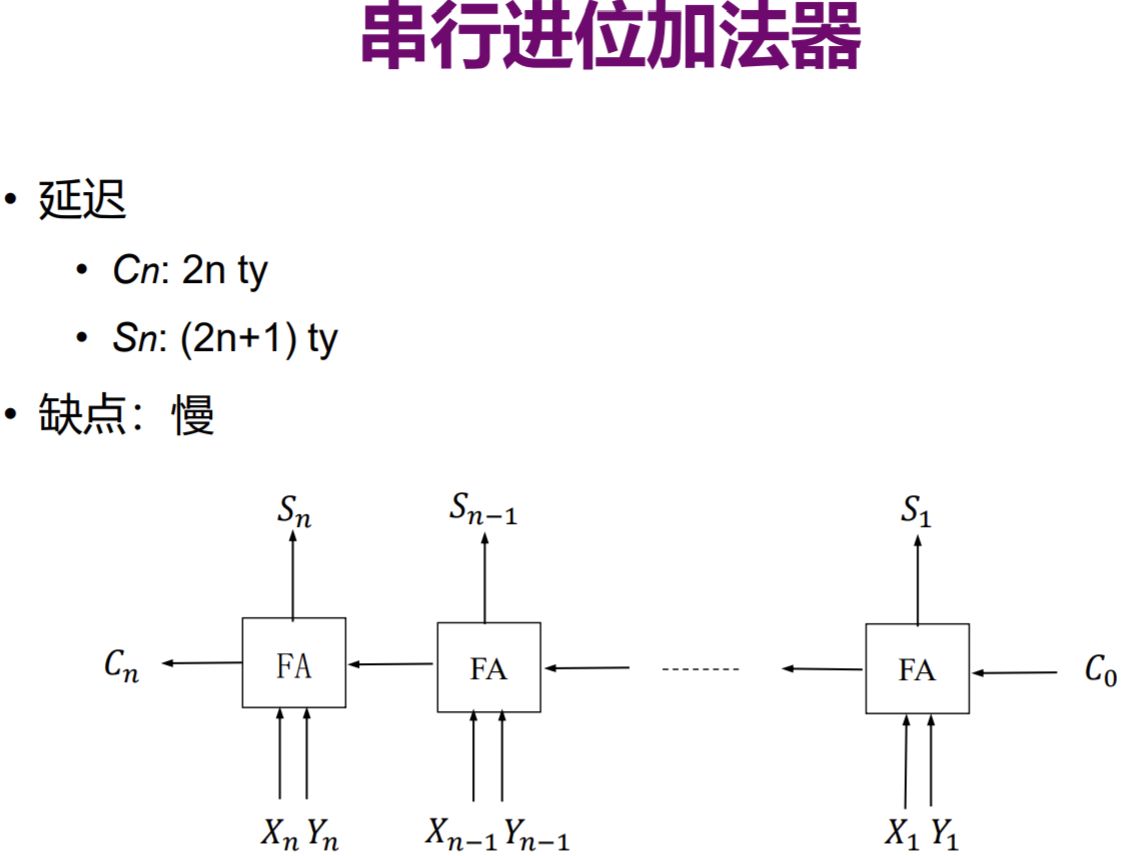
串行进位加法器

解释：

Cn = XnCn-1 + YnCn-1 + XnYn，由于每一次都需要前一个Cn-1，故与运算和或运算的时间均不可省略，为2*n ty = 2n ty

Sn = Xn^Yn^Cn-1，由于Cn-1在2（n-1）时刻已经准备好，同样的Xn^Yn可以早早计算好，故而只需等待到Cn-1即可再做一次异或运算，时间为2（n-1）+3=2n+1

特别的：发现S1计算时，X1^Y1花费3ty，（X1^Y1）^C0花费3ty，共花费6ty。S2计算时，得到C1需要2ty，得到（X2^Y2）需要3ty，等待（X2^Y2）结果，此时总共已经花费3ty，再做（X2^Y2）^C1又需要3ty，合计6ty。而按照公式计算所得结果S1应该延迟3ty，S2应该延迟5ty。why?

公式成立的前提是，假设所有的Xi^Yi自开始起便全部得出结果，共需要3ty，所以2（n-1）>= 3，即得出n >= 5/2，所以不难理解为什么S1、S2不符合了

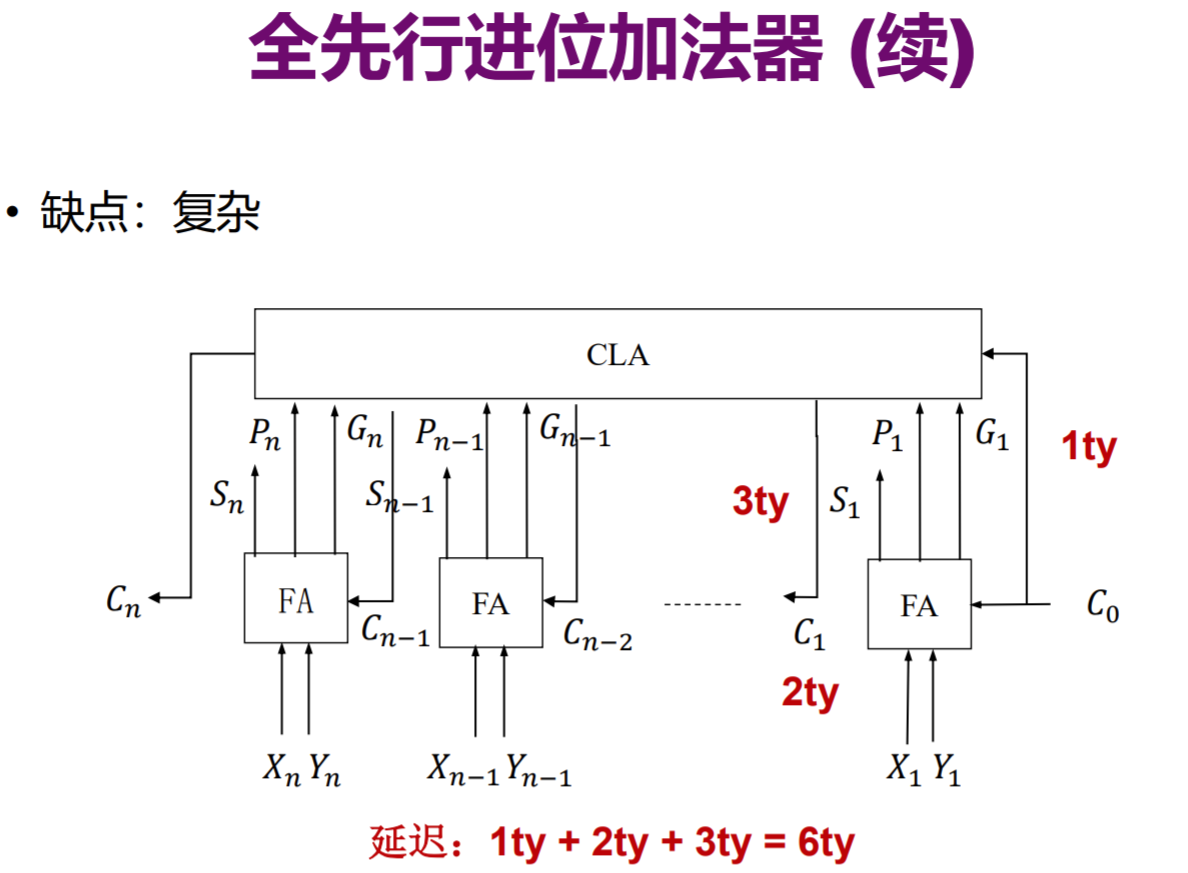
全先行进位加法器

通过刚才的过程已经发现，串行进位加法器的延迟与运算位数呈现线性关系，效率较慢，有什么方法减少延迟呢？

展开到最后竟然惊奇地发现，计算Cn并不需要Cn-1，也就说，每一个Cn都可仅用X、Y、C0这些已知数，做与运算以及或运算直接得出，（共需要2ty，错）其中计算出所有的P、G需要1ty，再进行一次大的与运算以及或运算，需要2ty，共需要3ty。

又同时可以进行Xi^Yi的操作，共需3ty，所以执行完上述两个过程共需3ty（可同时进行），再进行（Xi^Yi）^Ci-1又需要3ty，所以总共需要6ty

不难看出延迟大大降低，达到了常数。但，通常节省了时间，就不可避免要以空间的cost作为代价。多个与门，或门，结构复杂。

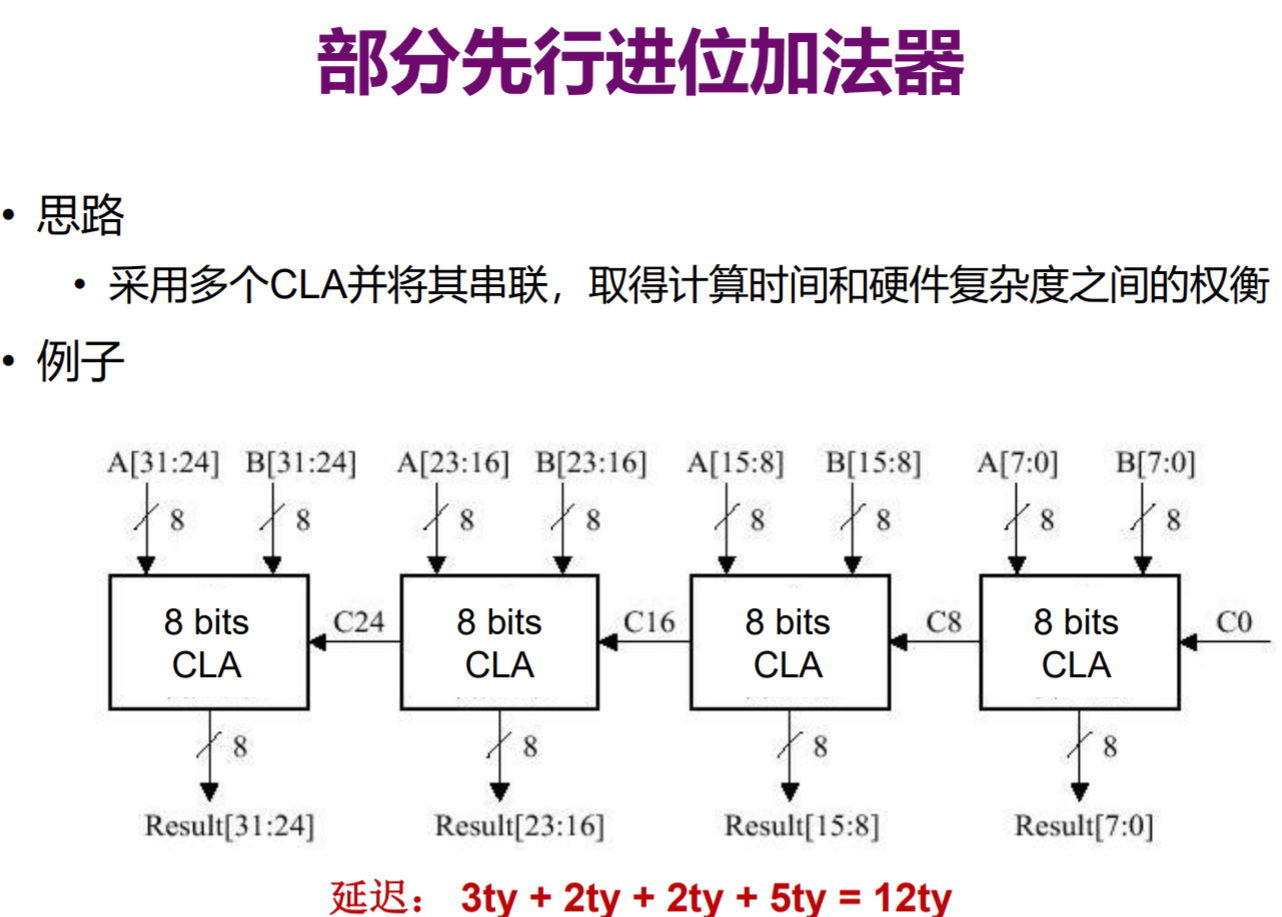
部分先行进位加法器

既然上述两种方案都有其缺陷，有没有什么可以综合的地方？部分先行进位加法器

计算所有的P、G需要1ty，计算C1-C8还需要2ty，完成第一个CLA中所有C的计算共花费3ty，由于所有P、G均在开始时计算得到，故二三四个CLA都只需要额外2ty延迟计算Ci，共需要3+2+2+2=9ty。同时，可以发现我们还没有考虑Si的计算。由于第四个进位加法器一定最后结束运算，得到Ci后，还需3ty做异或运算，其余CLA最迟也可以在同时计算Si，故一共还需要3ty延迟，共需9+3=12ty。

整数加法

补码表示相加，直接按位对应进行进位加法器相关的操作。

注意：什么情况下不适用？溢出！

众所周知，n位最多表示2^n个不同的数，可表示的数进行加法运算也就可能超过可表示的范围，既然不能表示，那得到的所谓“结果”自然是错误的。

什么时候会溢出？同号相加！

c = a + b，若a、b异号（假设a+,b-)，必然有 a > c > b，既然a、b均可表示，落在a、b之间的c自然可以表示

a、b同号时，做加法，就以一个最简单的例子，max+1即溢出，min+(-1）即溢出

溢出有什么特点？变号！

即所谓的Sn≠Xn,Yn。

为什么如此？

min+min=-2^n

max+max=2^n-2

溢出部分范围：以四位举例

max+1~2*max 1000~1110，第四位为1，异号

min-1~2*min 0111~0000，第四位为0，异号

回顾补码表示导入的这张表（当然表中0所示位置上方数值应为0），此时不难理解为什么溢出之后符号位改变了，正数继续前进则进入负数的范围，负数倒退则步入正数的范围内。

以下代码为整数加法运算的Java实现，但实现过程较为繁琐，依据全加器的原理，通过与运算、或运算、异或运算即可将全部情况进行计算。

/**
 * 返回两个二进制整数的和
 * dest + src
 *
 * @param src  32-bits
 * @param dest 32-bits
 * @return 32-bits
 */
public DataType add(DataType src, DataType dest) {
    // TODO
    String s1 = src.toString();
    String s2 = dest.toString();
    char[] result = new char[32];
    for (int i = 0; i < 32; i++){
        result[i] = '0';
    }
    for (int i = 31 ; i >= 0; i--){
        if(s1.charAt(i) == '0' && s2.charAt(i) == '0'){
            if(result[i] == '0'){
                result[i] = '0';
            }else {
                result[i] = '1';
            }
        } else if (s1.charAt(i) == '0' && s2.charAt(i) == '1') {
            if(result[i] == '0'){
                result[i] = '1';
            }else {
                if(i != 0){
                    result[i-1] = '1';
                }
                result[i] = '0';
            }
        } else if (s1.charAt(i) == '1' && s2.charAt(i) == '0') {
            if(result[i] == '0'){
                result[i] = '1';
            }else {
                if(i != 0){
                    result[i-1] = '1';
                }
                result[i] = '0';
            }
        } else {
            if (result[i] != '0') {
                result[i] = '1';
            }
            if(i != 0){
                result[i-1] = '1';
            }
        }
    }
    String out = new String(result);
    return new DataType(out);
}

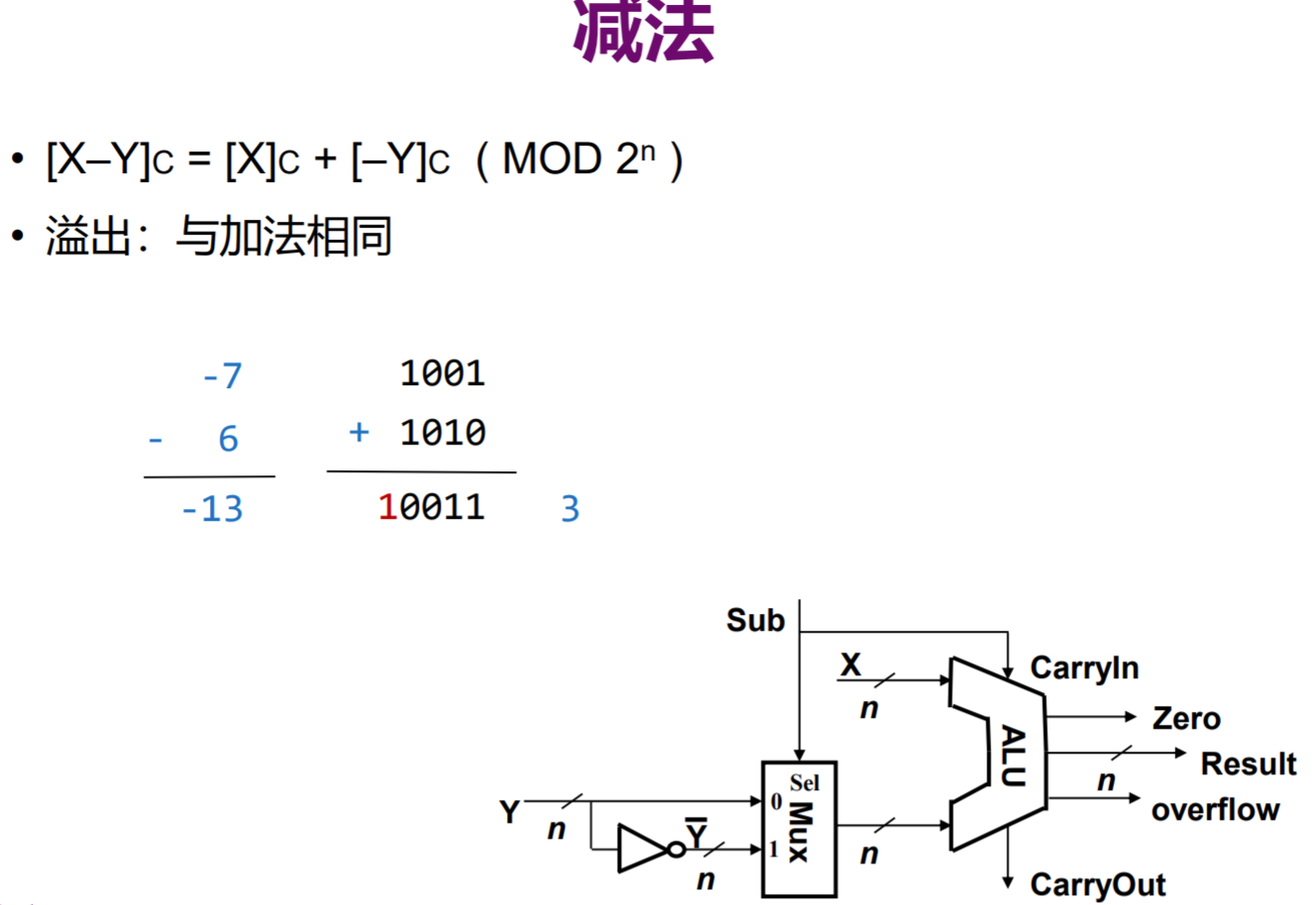
整数减法

减法不再加以赘述，理解为加法运算即可。

以下为整数减法实现的Java代码，所采取的是利用取反加一化为两数加法进行计算。

    /**
     * 返回两个二进制整数的差
     * dest - src
     *
     * @param src  32-bits
     * @param dest 32-bits
     * @return 32-bits
     */
    public DataType sub(DataType src, DataType dest) {
        // TODO
//        dest-src
        String src1 = src.toString();
        char[] src2 = new char[32];
        for (int i = 0; i < 32; i++){
            if(src1.charAt(i) == '0'){
                src2[i] = '1';
            }else {
                src2[i] = '0';
            }
        }
        String src3 = new String(src2);
        DataType result1 = add(new DataType(src3), dest);
        return add(result1, new DataType("00000000000000000000000000000001"));
    }

寄存器 && 内存

通过与门和或门可以制造出只存储0和1的电路来，将两个电路结合起来，形成锁存，Memory!

抽象上述概念，一个门锁包含输入和允许写入位，用以存储一位数据0 or 1

一组锁存器就形成了寄存器，一个寄存器能存储多少位宽的数字就是多少位的寄存器
当然我们可以采用锁存器并排放置，这需要2n+1条线，而将其制造成网格结构可以大幅减少线的数量，这时需要多路复用器锁定需要存取的位置

对于底层的复杂概念，再次将其封装抽象，得到一个如256bit的内存，有八位地址，一条允许写入线，一条允许读取线，一条数据线用于读、写

将八个上述的存储结构并行排列起来，一次就可以读写8bit的数字，也就是所谓的一字节，也就能够存储256字节大小的内容

再次抽象，将上述每八个存储单元抽象为一个内存地址所代表的一个8位数字，我们就有了256个可以寻址的8位数字

CPU

中央单元处理器，负责执行程序，程序由一个个操作组成，这些操作是一条条指令

取指令阶段->解码阶段->执行阶段

由不同逻辑电路解析不同指令，将这个整体抽象为一个控制单元

整合寄存器以及ALU就可以使得CPU取指、解码、执行对于内存，对于计算的操作了

引入时钟管理CPU节奏，时钟速度/Hz

居然还讲到超频了，之前虽有耳闻，原理却是第一次了解，提高时钟频率，加快处理速度，获得更加强劲的性能

所以CPU大致等于寄存器+控制单元+ALU+CLOCK

指令和程序

CPU是可编程的

引入更加多的指令，就可以使CPU做更多的事

为了表示更多的指令，所想到的两个有效措施，一是增加用以表示指令的位数，二是使用可变长的指令长度

英特尔4004处理器不过只能支持46个指令，而如今（如果chatgpt没说胡话的话）x86架构的CPU已经支持2000多条指令集

高级CPU设计

复杂度 vs 速度的平衡在计算机发展史上经常出现，确实

不断设计更为便捷的指令，同时兼容旧的指令

CPU处理速度与内存读取速度之间拉开差距（也就是机组中所讲的内存墙），在CPU内部引入cache

进一步减少CPU空闲时间，使用流水线方式

在条件跳转指令可能等待大量时间时，采取分支预测，甚至如今已经有90%概率猜对将要选择的路径

多核、多CPU、超级计算机